Plants need a certain amount of water to thrive. For lawns, calculate about 1 inch of water per week that each patch of lawn needs to receive. In very hot periods even about 20 percent more. The precipitation rate indicates how much water is poured in one hour. It is therefore the basis for determining the correct duration of irrigation. In the following blog post you can find out how to calculate the precipitation rate yourself or how to recognize the assumption under which it was calculated.
Calculation for an already active irrigation
If the irrigation is already in operation, the easiest way to determine the precipitation rate is to compare the amount of water used and the area irrigated. This should be done separately for each irrigated sector, as the results can differ significantly. You can either simply read the amount of water from an already installed water meter, or you can get a water meter and install it after the water source. You can let the watering run for a whole hour and then compare the meter reading with the one at the beginning of the watering, or you can just let it run for a shorter time and then extrapolate to one hour. The area is either known or can otherwise be determined with a measuring tape.
Calculation formula Precipitation rate = gallon output per hour/area in square foot
In order for the calculation to work, the denominator and counter must be brought to the same units. The following applies:
- 1 gallon water = 231 inch3
- 1 foot2 = 144 inch2
So if you water, for example, an area of 20 by 20 feet with 300 gallons water for an hour, then it would apply:
Precipitation rate = 300 * 231 inch3/20 * 20 * 144 inch2 = 69,300 inch3/57,600 inch2 = 1.20 inches
Attention: This value is an average value and says nothing about how evenly this precipitation is distributed over the area. It may be that some spots receive significantly more water than others, depending on how professionally you have planned your watering (see “square pattern” and “triangular pattern” in the next point).
The rest of the considerations are easy: how much water does the irrigated area need per week and how do you divide up the watering? If you pour the amount of water collected in one irrigation run per week, then you simply divide the required amount of water by the capacity of the irrigation system per hour and thus know the required running time. In the example above, the irrigation system is pouring 300 gallons per hour over a 400 square foot area, which is 0.75 gallons per square foot. The lawn is to receive 0.6 gallons per square foot per week, so watering must run for 1.25 hours (0.75/0.6). So an hour and 15 minutes. If you water twice a week, that would be two times 37 minutes.
Water flow meters at Amazon:
Auto Amazon Links: No products found. No products found.
Calculation for a planned irrigation
The sprinklers are positioned in a professional planned irrigation either in the square pattern or in the triangular pattern. The calculation of the precipitation rate also depends on the selected system, whereby the precipitation rate of the triangular pattern is about 10 to 15 percent higher in comparison due to the somewhat higher overlap.
For most sprinkler suppliers, the precipitation rate for both patterns is included in the product descriptions (the triangle symbol indicates the triangular pattern, the square symbol indicates the square pattern). The precipitation rate is given for different water pressure values, which affect the radius and flow rate of the sprinkler and thus also cause a different precipitation rate. An overview of this performance data for numerous sprinklers can be found on the sprinkler performance data page.
Calculating the rate of precipitation in the square pattern
As in the triangular pattern, the following values are required for the calculation:
- The radius of the sprinkler
- The flow rate of the sprinkler
Formula to calculate the flow rate in the square formation = flow rate/(radius*radius)
This formula is best understood using a single square of the square pattern:
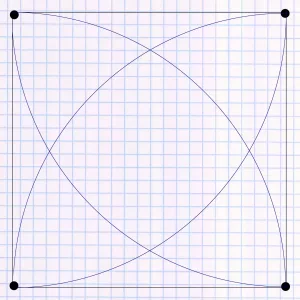
Area irrigated in square pattern
The height and width of the square corresponds to the throw distance (radius) of the sprinkler. It receives water from 4 sprinklers in total (marked as black dots in the corners). And each sprinkler waters a quarter circle of the square.
Let’s take the Gardena T200 as an example: This has a flow rate of 150 gallons/hour and a throw distance of 26 feet in 360 degree operation at 29 psi pressure. Before you can calculate, these values have to be converted to the common unit of inches. Again the following applies:
- 1 gallon water = 231 inch3
- 1 foot2 = 144 inch2
The flow rate in the square pattern would thus be 150*231/(26*26*144) = 0.36 inches.
This calculation is correct if one assumes that the area is irrigated with sprinklers that irrigate in a full circle. And it is also true for sprinklers with built-in MPR principle such as the Hunter MP-Rotator and for sprinklers that are operated with MPR nozzles. For all of these, the flow rate of a sprinkler is used in the full circle principle. It is therefore assumed that the irrigation looks like this:
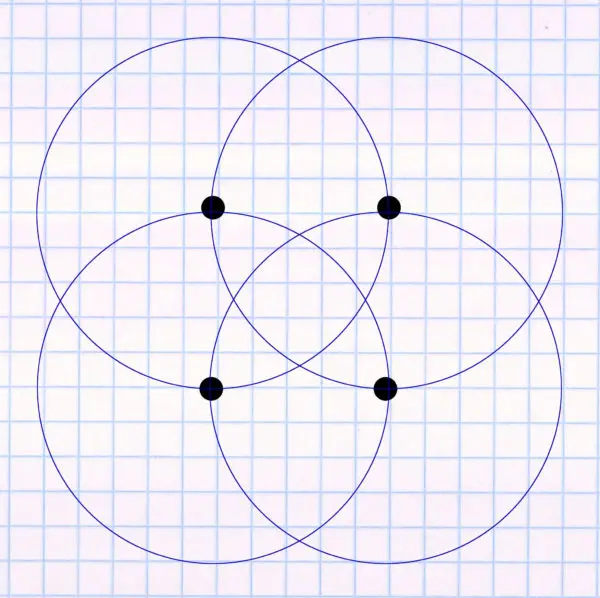
Area irrigated in square pattern (within the 4 black dots). The sprinklers irrigate full circles
So each sprinkler that acts on the square runs a full circle. Why is this important? For sprinklers that do not have the MPR principle built in and are not used with MPR nozzles, the precipitation rate is directly related to the circle sector that the sprinklers irrigate. It’s easy to explain why: These sprinklers always release a certain amount of water in a certain amount of time, say 150 gallons per hour. If the sprinkler runs a full circle, it will spread that 150 gallons over the full circle. If, on the other hand, it only runs half a circle, then it runs twice its half circle in the time in which the sprinkler previously ran the whole circle and the lawn in this area receives twice as much water in the same time. With a quarter circle it would even be four times as much. Therefore, with the exception of the MPR sprinklers mentioned above, it is relevant when planning how the irrigation is planned, whether sprinklers irrigate full circles or sprinklers irrigate semicircles. If you plan to use full-circle sprinklers, then the above formula is correct. If you plan your sprinklers to irrigate semicircles or quarter circles, then the result must be multiplied by 2 or 4. So the correct formula is:
Formula to calculate the square pattern for operation in a semi-circle (180 degree sector) = 2*flow rate/(radius*radius)
Formula to calculate the square pattern for operation in a quarter-circle (90 degree sector) = 4*flow rate/(radius*radius)
For this reason, the sprinkler manufacturers indicate in their description for which operation it was calculated. This is mostly for operation in the 180 degree sector, but with some sprinklers also in the 360 degree sector. It is therefore very important to bear this in mind, otherwise the actual precipitation rate may be half or double what is stated in the description.
Derive missing manufacturer information yourself
Sometimes it happens that this information, whether the precipitation rate was calculated with 180 degrees or 360 degrees, is missing for one or the other sprinkler type. This is no problem for you with the formulas given here: Simply take the flow rate and the throw distance and enter them once in the formula for full-circle sprinklers and once in the formula for half-circle sprinklers. Compare the result with the information provided by the manufacturer and you will know which of the two variants was used to calculate it. The same applies to the calculation in the triangle pattern (see next point).
Calculating the rate of precipitation in the triangular pattern
In principle, the same applies here as described above. The two values throw distance (radius) and flow rate are also required, only the formula for the calculation is slightly different:
Formula to calculate flow rate in triangular pattern = radius/(throw*(throw*0.866))
Let’s take again the example of the Gardena T200 with a flow rate of 150 gallons/hour and a radius of 26 feet and again the following applies:
- 1 gallon water = 231 inch3
- 1 foot2 = 144 inch2
The flow rate in the triangular pattern would thus be 150*231/(26*(26*0.866)*144) = 0.41 inches
How can the formula be understood? In the triangular pattern, a pattern of many equilateral triangles emerges:
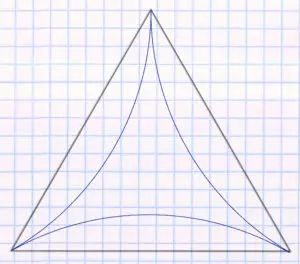
Area irrigated in triangular pattern
In the triangle pattern, each triangle receives water from 6 different sprinklers. The triangle is equilateral, meaning that each of the sides is the same length and the triangle is perfectly symmetrical. And it means that the height of the triangle is 86.6 percent of the side’s width. That’s the 0.866 in the formula above. The area is calculated by multiplying the length of the side by the height.
As before, it is also relevant here whether the sprinklers are operated in the 360 degree circle or in a 180 degree or 90 degree circle. For the 180 degree or 90 degree circle, multiply by 2 or 4 as before:
Formula to calculate the triangular pattern for operation in a semi-circle (180 degree sector) = 2*flow rate/(radius*(radius*0.866)
Formula to calculate the triangular pattern for operation in a quarter-circle (90 degree sector) = 4*flow rate/(radius*(radius*0.866)