The correct placement of the sprinklers on the area to be irrigated is one of the most important points when planning an irrigation system. Firstly, this is crucial for watering the garden as evenly as possible and consequently saves water. And secondly, incorrect positioning can often only be corrected later with great effort.
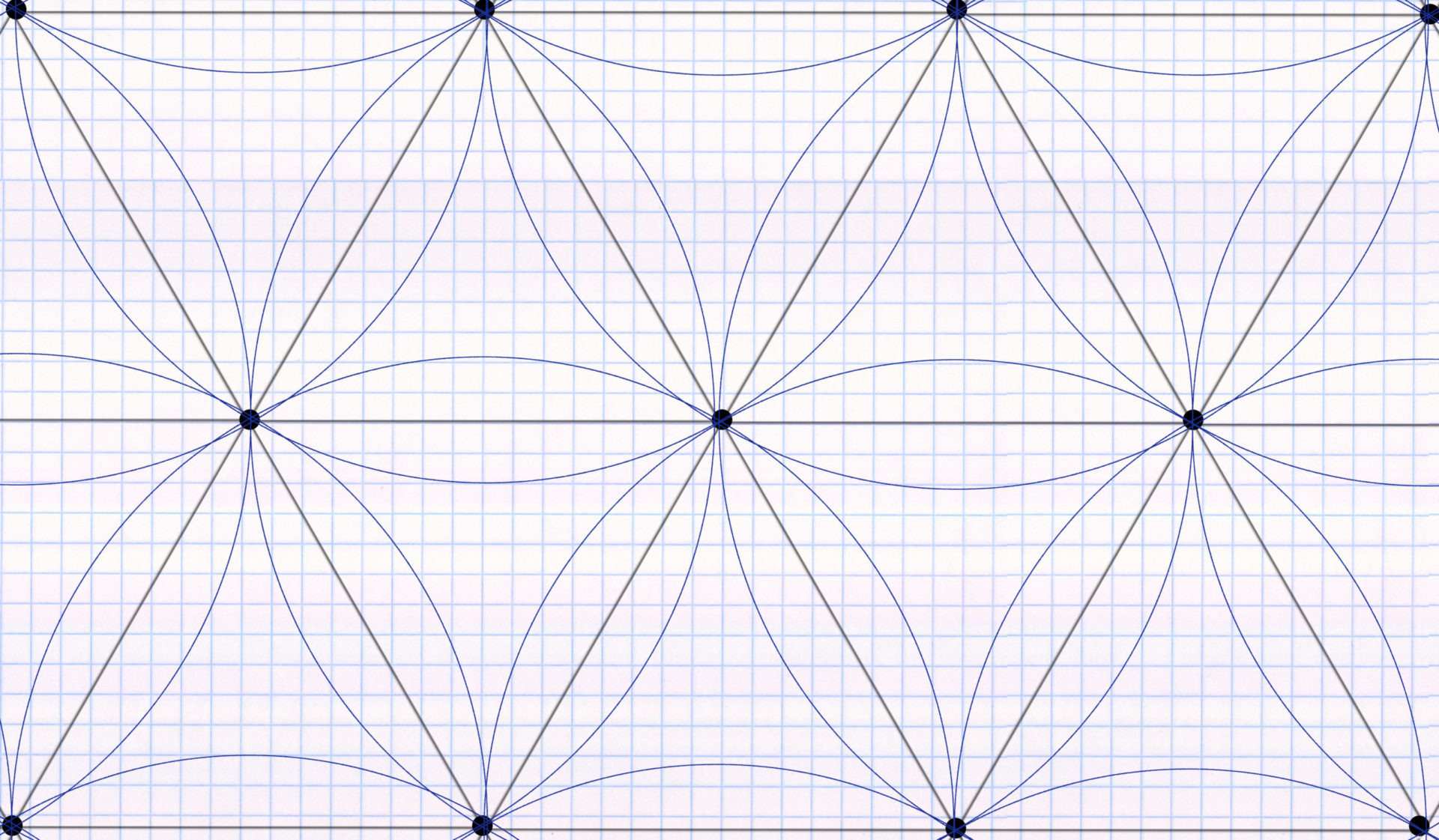
When positioning sprinklers, a distinction is made between a square pattern and a triangular pattern. These two are the dominant principles around the world by which most irrigation is planned. The square pattern described below is the technique that is somewhat easier for the user to implement and is particularly suitable for rectangular areas. In the following blog post you can find out how it works, what its advantages are and how the square pattern is reflected in the performance data of the sprinkler manufacturers.
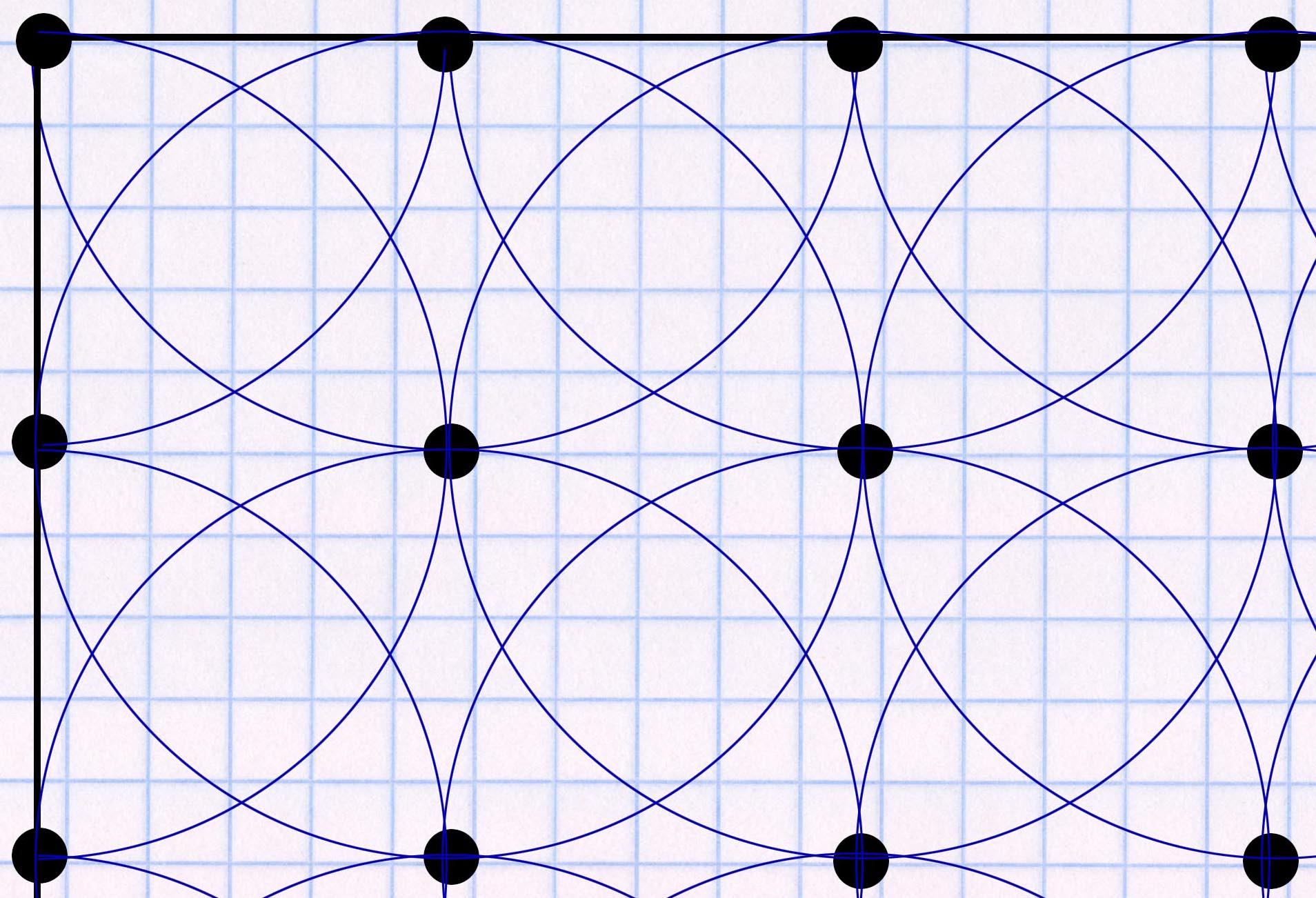
The basic principle of the square pattern is the principle of double overlap: each sprinkler must be reached by the throwing circles of (at least) two other sprinklers. For example, this can look like this for a square basic shape:

A sprinkler is placed in each corner. This is reached by the throwing circle of its left and right neighbor sprinkler (= double overlap). On the planning page you will find further examples for the placement of sprinklers in different basic shapes.
In the square pattern, 4 sprinklers are placed in such a way that – if you mentally connect the sprinklers – a square results. These 4 sprinklers together correctly cover the square area they enclose – according to the rules of the square pattern. The distance between the sprinklers in the square pattern is approx. 50% of the sprinkler throw diameter, i.e. approx. the throw range (= radius) of the sprinkler. For example, if you have a 30 foot throw, the sprinklers will be positioned 30 feet apart.
Before starting, the ground plan of the garden – if it does not already consist of a square or a rectangle – is divided into rectangular parts. You can find an example of this in the planning section. When drawing in, start with the trickiest spots – these are the 4 corners of the area to be watered. A sprinkler is placed in each of these, throwing a quarter circle:

Next, proceed to the second most delicate area: the edges. The sprinklers are set on the edges with half-circles in such a way that they correctly overlap their right and left neighbor sprinklers. Your throwing circle must therefore reach to the neighboring sprinklers. It then looks like this:
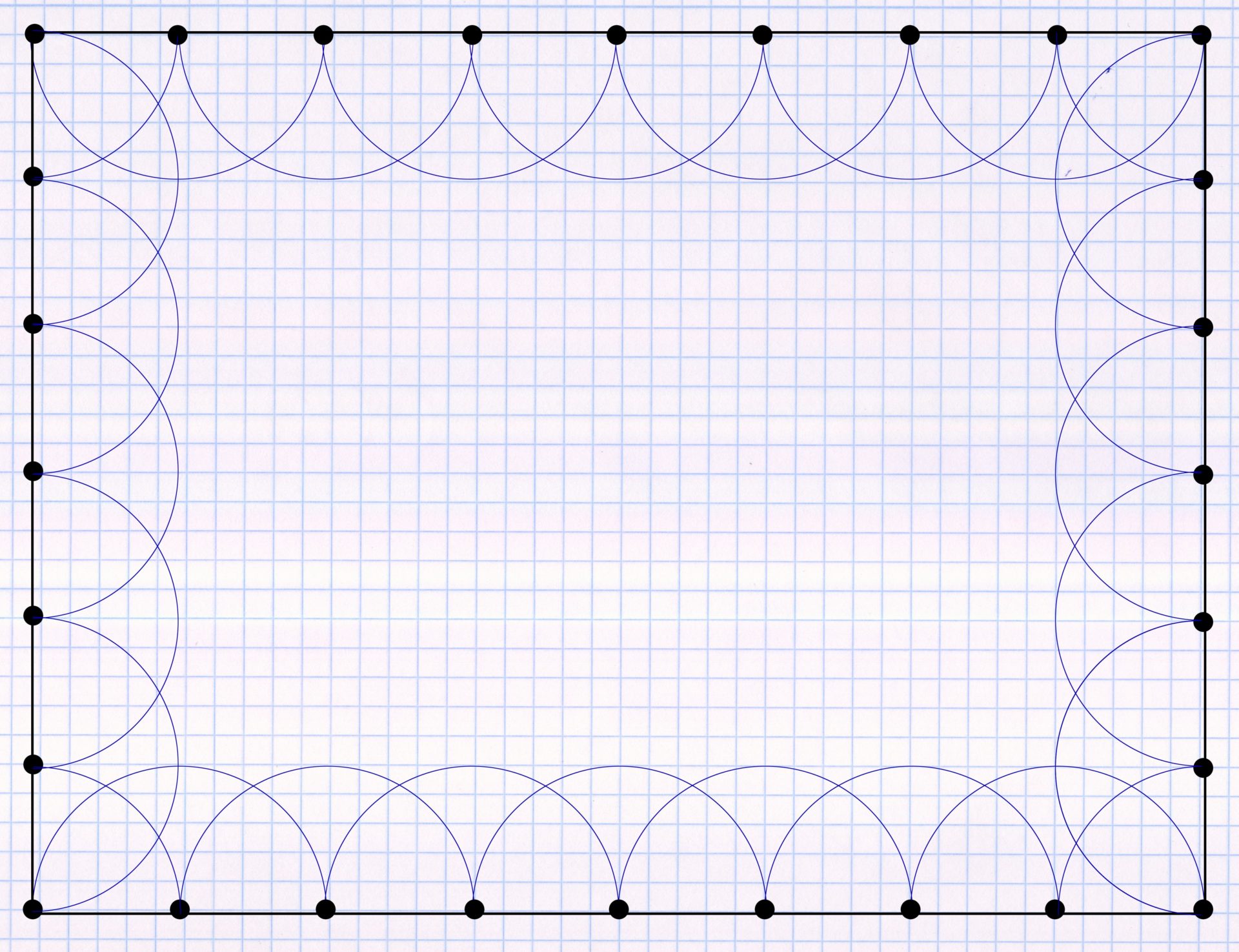
Before drawing in the other sprinklers, you can make auxiliary lines. To do this, connect each of the sprinklers on the edge, with the exception of the corner sprinklers, to the sprinkler on the opposite side. On the plan, this results in a checkered pattern:

Full-circle sprinklers are now drawn in at the intersections of the auxiliary lines. After the first circumnavigation it looks like this (I have removed the auxiliary lines for the purpose of a clearer representation):
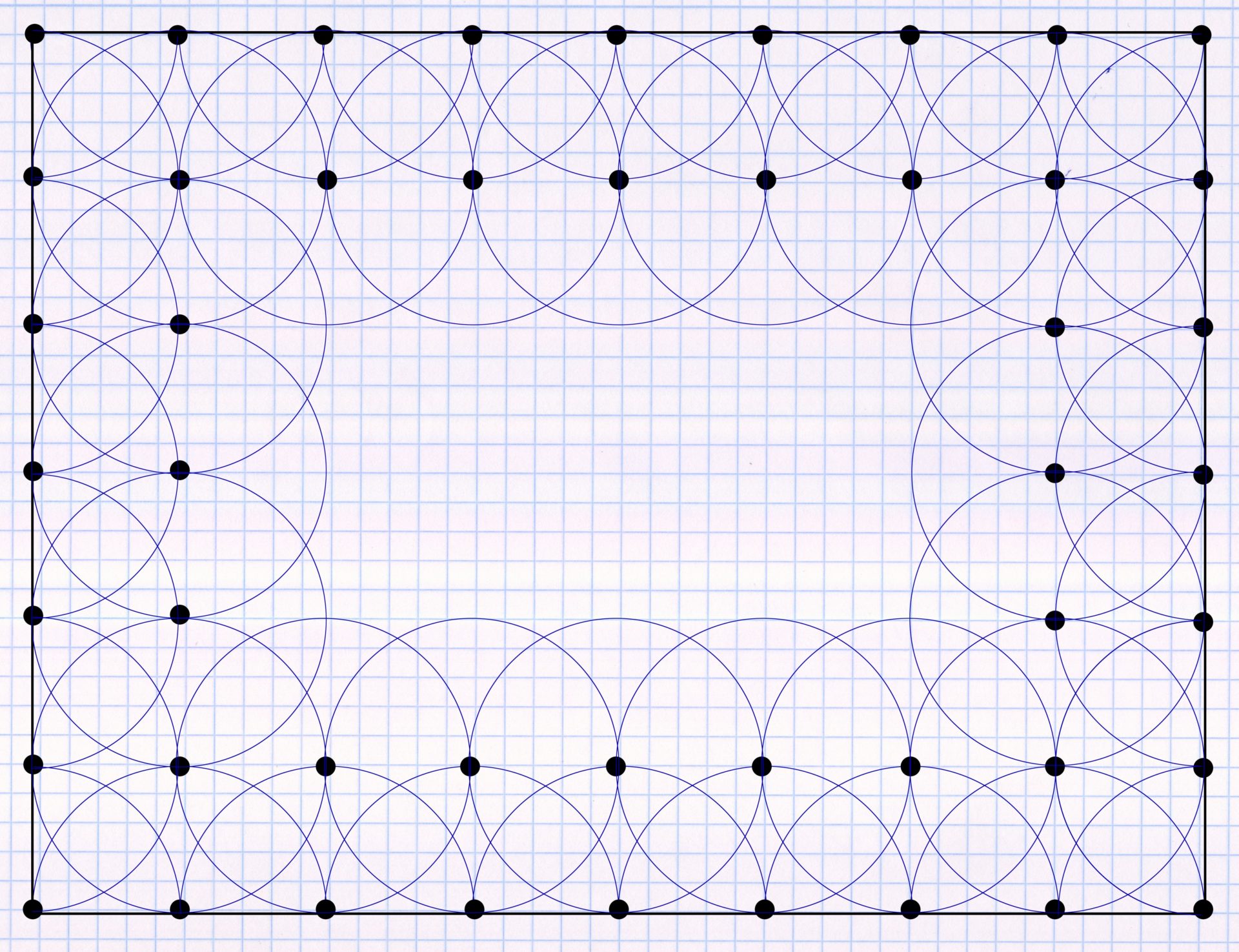
An unirrigated spot remains in the middle. This is now also filled with full circles. This ultimately leads to the following result:
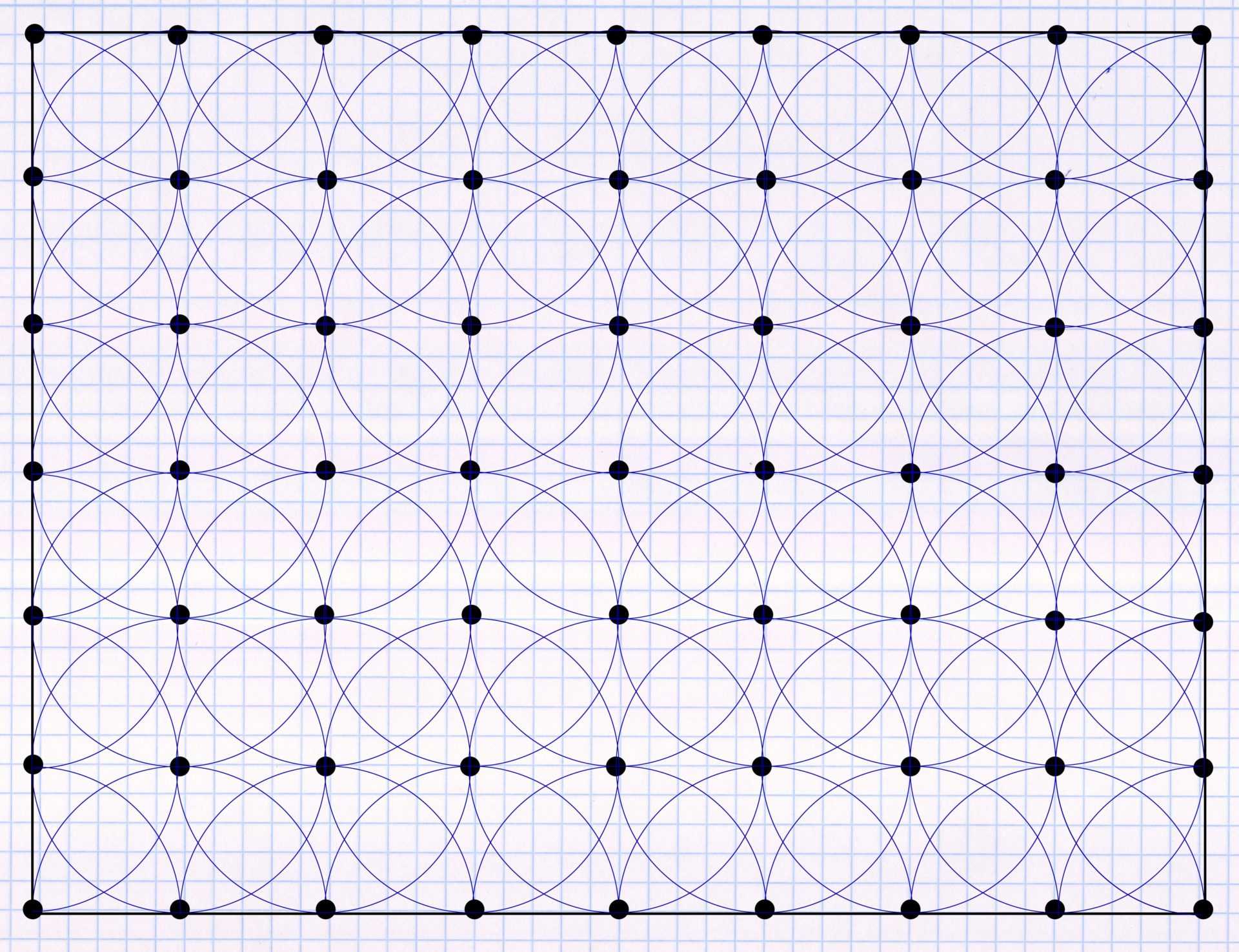
You can see that there is a continuous pattern over the entire irrigation area, which always looks exactly the same within 4 sprinklers. This consistent pattern means the lawn is watered evenly across the entire area. This means that all areas of the lawn receive the same amount of water.
In my example, it is exactly the case that the set full and semicircles result in exactly the length and width of the area to be irrigated. In practice, this often does not turn out so well, so that, for example, a horizontal and/or vertical area remains that is only half the diameter of the circle, for example. Here you can then either strictly follow the principle further and thus accept a larger than planned overlap at this point. Or you try to cushion this effect of the additional overlap by reducing the throwing circle or choosing smaller nozzles for the sprinklers in question in order to achieve the same amount of precipitation as possible as in the other squares. A third possibility is the use of MP Rotator sprinklers, which independently keep the amount of precipitation constant (more on this below in the chapter “Sprinklers with integrated MPR function”).
Reference to square and triangle pattern in sprinkler operating data
The sprinkler manufacturers indicate the precipitation rate for their sprinklers in their product descriptions. This is done for a specific water pressure and a specific nozzle used with reference to the square or triangle pattern. Following is an example:
Rain Bird 3500 Series
| Nozzle | Water Pressure | Radius | Flow | Precipitation inches/hour ∎ | Precipitation inches/hour ▲ |
|---|---|---|---|---|---|
| 2,0 | 25 psi | 27 feet | 84 gallons/hour | 0.37 inches/hour | 0.43 inches/hour |
| 2,0 | 35 psi | 27 feet | 101 gallons/hour | 0.45 inches/hour | 0.52 inches/hour |
| 2,0 | 45 psi | 27 feet | 116 gallons/hour | 0.51 inches/hour | 0.59 inches/hour |
If you irrigate according to the principle of the square pattern, then the lawn receives 0.37 inches of precipitation per hour at 25 psi. This corresponds to 0.23 gallons per square foot.
Note: The 0.23 gallons per hour does not refer – as is often wrongly believed – to the one sprinkler listed on its own, but is only achieved if this sprinkler is operated together with others in a square pattern. So if there is a proper overlap. The one sprinkler on its own would have a much lower precipitation rate, which would be only a fraction of what it was advertised to be! You can calculate this relatively easily by calculating the area of the circle and then dividing the flow rate by the area. In the example, with a throw distance of 27 feet, we would have a full circle with an area of 2,289 square feet (27 x 27 x 3.14). If you divide the amount of water available per hour of 84 gallons by the number of square feet, you would arrive at a rainfall of just 0.037 gallons/hour per square feet. Even if you operate the sprinkler not as a full circle but as a quarter circle, only 0.15 gallons per hour would result.
Adjust precipitation – use of appropriate nozzles
When placing the sprinklers, you must ensure that the amount of precipitation from the sprinklers must be adjusted depending on the size of the sector of the circle. Why? Most sprinkler models always release the same amount of water in a certain amount of time, e.g. 200 gallons/hour at 30 psi pressure. If the sprinkler is set to full circle, it would distribute these 200 gallons in a full circle. The sprinkler starts at a certain point and then slowly rotates until it has completed the full circle. Then he does it all back in the opposite direction. If the sprinkler was set to a quarter circle, it would also pour 200 gallons per hour, but spread the water over an area that is only a quarter as large. The areas irrigated with a quarter circle would receive four times as much water in the same period as the areas irrigated with a full circle. And the areas irrigated with a semicircle would get twice as much as those irrigated with a full circle.
This effect is compensated for by the nozzle size of the sprinkler. So you change the nozzles of the sprinklers in order to have the same precipitation rate for everyone. The semi-circle sprinklers have nozzles with twice the flow rate as the quarter-circle sprinklers. And the full-circle sprinklers have nozzles with twice the flow rate of the half-circle sprinklers. In our example, the full circle sprinkler would pour 200 gallons per hour, the half circle sprinkler about 100 gallons and the quarter circle sprinkler about 50 gallons per hour. Each quadrant would therefore get the same amount of water of about 50 gallons per hour. The sprinkler manufacturers usually reflect this system in the classification of their nozzles: A No. 4 nozzle has twice the flow rate as a No. 2 nozzle a No. 8 nozzle has twice the flow rate as a No. 4 nozzle.
So you could think that the quadrant sprinklers could simply be equipped with No. 2 nozzles, those with a semi-circle with No. 4 nozzles and those with a full circle with No. 8 nozzles and thus achieve the same precipitation rate for all. Unfortunately, it’s not quite that simple! The problem is that using different nozzle sizes also affects the throw distance of the sprinklers. With the same water pressure, larger nozzles lead to greater throw distances, smaller nozzles to shorter throw distances. It is therefore not possible to depict a correct square or triangle pattern in this way, since the same throwing distances are required for these, regardless of the size of the sector of the circle!
The sprinkler manufacturers have solved this problem with the introduction of so-called MPR nozzles. MPR stands for “Matched Precipitation”, i.e. the principle of matching the precipitation rate to one another. An MPR nozzle set contains 4 nozzles for 90 degrees, 120 degrees, 180 degrees and 360 degrees. Depending on which section of a circle you want to sprinkle, you use the appropriate nozzle in the sprinkler. This not only adjusts the precipitation rate, but also results in an identical throw distance. All 4 included nozzles therefore have the same precipitation rate and throw distance at the same water pressure.
Important: When choosing a sprinkler, make sure that the sprinkler is MPR-capable! This only applies to the newer model generations, older sprinklers cannot handle MPR nozzles or MPR nozzles are not available for them at all.
A possible alternative to adjusting the precipitation rate using MPR nozzles would be to group together sprinklers with the same sized circular sections in one sector and to achieve the same amount of precipitation over different irrigation times. So let the sector with the full-circle sprinklers run 4 times as long as the one with the quarter-circle sprinklers.
Sprinklers with integrated MPR function
Hunter’s MP Rotator sprinklers go one step further. These already have the MPR function built in: If you adjust the radius or the circular section to be irrigated, the sprinkler automatically adjusts the water flow to the same extent, so that you always have the same precipitation rate. In addition, the precipitation rate of the MP-Rotator is always the same for all models, so that different models can be mixed in one sector without any problems.
Below is a link to MP Rotator sprinklers and the associated bodies on Amazon: